Bağıntı Nedir?
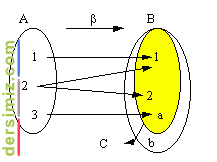
Kümelerin kartezyen çarpımının bir alt kümesi. A ve B_kümelerinin C kartezyen çarpımı sayı ikililerinden oluşur. Bu C kümesinin § (beta) ile gösterilen tüm alt kümeleri A'dan B'ye birer bağıntıdır. Örneğin A= {1,3,5} ve B= {2,4} kümelerinin kartezyen çarpım kümesi C= {(1,2), (1,4), (3,2), (3,4), (5,2), (5,4)} dir ve C'nin sözgelimi ß= {(1,2), (3,4), (5,2)} alt kümesi bir bağıntıdır. A kümesi kendisiyle kartezyen çarpılırsa §'nın A'da bir bağıntı olduğu söylenir. Bağıntının, dört özelliği vardır: A'daki bir ß bağıntısında her (x,y) ve (y,z) bir elemanken (x,z) de bağıntının elemanı oluyorsa bağıntı "geçişken"dir; her (x,y) elemanı için (y,x) de §'nın elemanı oluyorsa bağıntı "simetrik"tir; x ile y birbirinden farklı oldukça (x,y) ve (y,x) ikililerinden en çok biri ß'nın elemanı oluyorsa bağıntı "ters-simetrik"tir ve A'nın her x elemanı için (x,x) ikilisi ß'nın elemanı oluyorsa bağıntı "yansıyan"dır. Örneğin, A kümesi bir ailenin bireylerini, ß bağıntısı da kardeşlik ilişkisini göstersin. Küçük ortancanın, ortanca da büyüğün kardeşiyken küçükle büyük de kardeş olacaklarından bu bağıntı geçişkendir. Ayrıca, küçük ortancanın kardeşiyken ortanca da küçüğün kardeşi olduğuna göre simetri özelliği de taşır. Örneğin gerçel sayılar kümesindeki büyüklük bağıntısı terssimetri özelliğini sağlar; çünkü x,y'den farklı oldukça ya x>y ya da y>x'tir. Eşitlik bağıntısınınsa yansıma özelliğine sahip olduğu kolayca gösterilebilir.


